Aula de Matemática de Quarta-Feira

 

                                Multiplicação de Polinômios

Resumo sobre multiplicação de polinômios

• A multiplicação de polinômios é uma operação em que cada termo do primeiro polinômio é multiplicado por cada termo do segundo polinômio.
• Os conceitos fundamentais aplicados na multiplicação de polinômios são: a regra de sinais, a propriedade distributiva e a propriedade da multiplicação entre potências de mesma base.
• A regra de sinais determina que o produto entre termos de mesmo sinal resulta em um termo positivo e o produto entre termos de sinais diferentes resulta em um termo negativo.
• A propriedade distributiva estabelece que:

a . ( b + c ) = a . b + a . c

Multiplicação entre monômio e polinômio

Na multiplicação entre monômio e polinômio, devemos empregar a propriedade distributiva entre o monômio e cada um dos termos do polinômio. Nesse caso precisamos considerar a multiplicação entre as partes literais. Caso as potências de x multiplicadas possuam a mesma base, o resultado deve manter a base e somar os expoentes.

Exemplo 1:

7x ⋅ (-x² -3) = 7x ⋅ (-x²) + 7x ⋅ (-3) = -7x³ - 21x

Exemplo 2:

(4x³ + 9x² -x + 1) ⋅ (x²) = 4x³ ⋅ x² + 9x² ⋅ x²+ (-x) ⋅ x² + 1 ⋅ x²

 = 4x5 + 9x4 - x3 + x²

Multiplicação de polinômio por polinômio

Na multiplicação de polinômio por polinômio, devemos empregar a propriedade distributiva multiplicando cada termo do primeiro polinômio por cada termo do segundo polinômio. Note que é o mesmo sistema utilizado na multiplicação entre monômio e polinômio.

Exemplo:

(x4+10) ⋅ (2x³+x) = x4 ⋅ (2x³+x) + 10⋅ (2x³+x)

=x4 ⋅ 2x³ + x4 ⋅ x + 10⋅2x³ + 10 ⋅ x

=2x7 + x5 + 20x³ + 10x

1. Responda:

As medidas do comprimento, da largura e da altura de uma caixa estão indicadas na imagem a seguir:

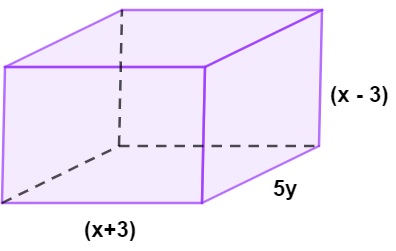
Analisando a imagem, podemos afirmar que o polinômio que descreve o volume da caixa é:

A) 5x²y + 30xy + 45y

B) 5x²y – 30xy + 45y

C) 5x² – 45y

D) 5x²y – 45y

E) 15xy + 3

2.