Números Irracionais e Números Reais
Os números irracionais são números decimais não exatos, que possuem representação infinita e não periódica e que não podem ser escritos como frações. Da união do conjunto dos números irracionais com o conjunto dos números racionais surge o conjunto dos números reais.

Como vimos logo no início do texto, os números irracionais são números decimais não exatos, que possuem representação infinita e não periódica e que também não admitem ser escritos como frações com numerador e denominador inteiros. Para compreendermos essa definição com clareza, vamos analisar alguns números irracionais.
√2 = 1,41421356237309504880168872…
√3 = 1,73205080756887729352744634…
Reparem nos números irracionais acima, que as casas decimais não terminam, são infinitas e completamente aleatórias. Isso significa que não há uma periodicidade ou uma sequência entre os algarismos dispostos após a vírgula, e que também não há como saber quais algarismos compõem as casas decimais representadas pelas reticências. Essas incertezas sobre o comportamento das casas decimais dos números irracionais nos impedem de representa-los sob a forma de fração.
Assim, podemos afirmar, por exemplo, que todas as raízes quadradas extraídas de números que não são quadrados perfeitos são números irracionais. Outro bom exemplo de número irracional é o famoso “pi” (π). Seu valor numérico possui infinitas casas decimais, sem que haja qualquer periodicidade entre os seus algarismos. O valor de π é oriundo da razão entre o comprimento de uma certa circunferência e o seu diâmetro.
π = 3,14159265…
2.1 O conjunto dos números irracionais em forma de diagrama
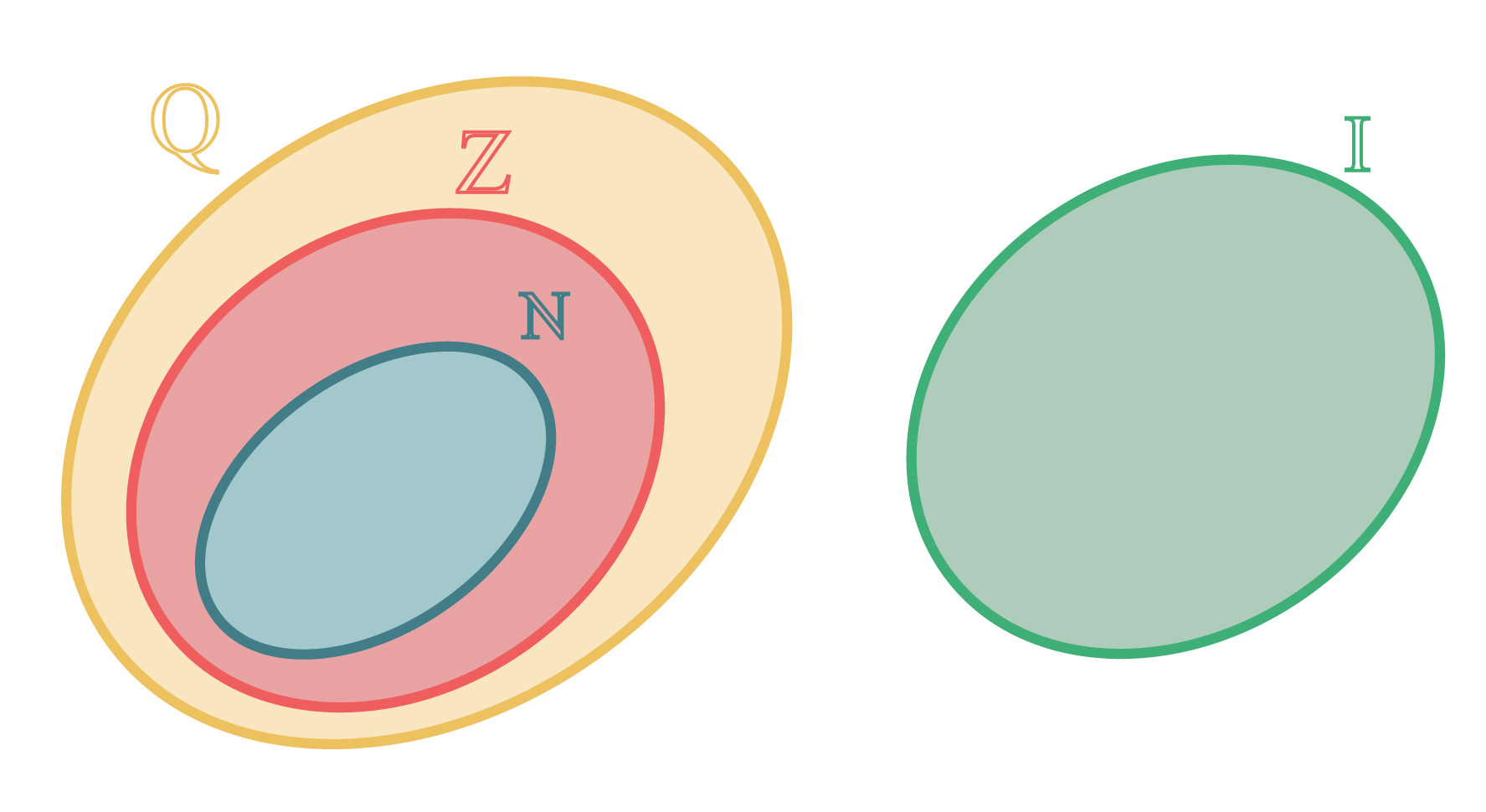
No decorrer deste texto, nós estudamos dois temas importantes dentro dos conjuntos numéricos. O primeiro deles, é que todos os números naturais e inteiros, assim como os decimais exatos e as dízimas periódicas são considerados números racionais. Isso nos permite concluir que os números naturais (ℕ) e os números inteiros (ℤ) são subconjuntos do conjunto dos números racionais (ℚ).
O segundo, e principal tema estudado aqui, é que o conjunto dos números irracionais (𝕀) é completamente diferente do conjunto dos números racionais. Esses dois conjuntos não possuem elementos em comum. Por isso, diz-se que eles são conjuntos disjuntos, e que a intersecção entre esses dois conjuntos resulta em um conjunto vazio.
ℚ ⋂ 𝕀 = ∅
De acordo com essas informações, podemos realizar a representação na forma de diagrama dos conjuntos apresentados como mostra a imagem acima.
CONJUNTO DOS NÚMEROS REAIS

O conjunto dos números reais (ℝ) é formado pela união entre o conjunto dos números racionais e o conjunto dos números irracionais. Assim, quando for necessário se referir a todos os números de maneira geral, sem excluir aqueles que podem ou que não podem ser representados na forma de fração, estaremos falando dos números reais.
ℝ = ℚ ⋃ 𝕀
ℝ = {x | x ∈ ℚ ou x ∈ 𝕀}
Dessa maneira, é possível completar a representação em forma de diagrama que realizamos no item anterior. Reparem que todos os demais conjuntos estudados estão localizados dentro do diagrama do conjunto dos números reais. Não podia ser diferente, afinal, números naturais, inteiros, racionais e irracionais também são números reais.
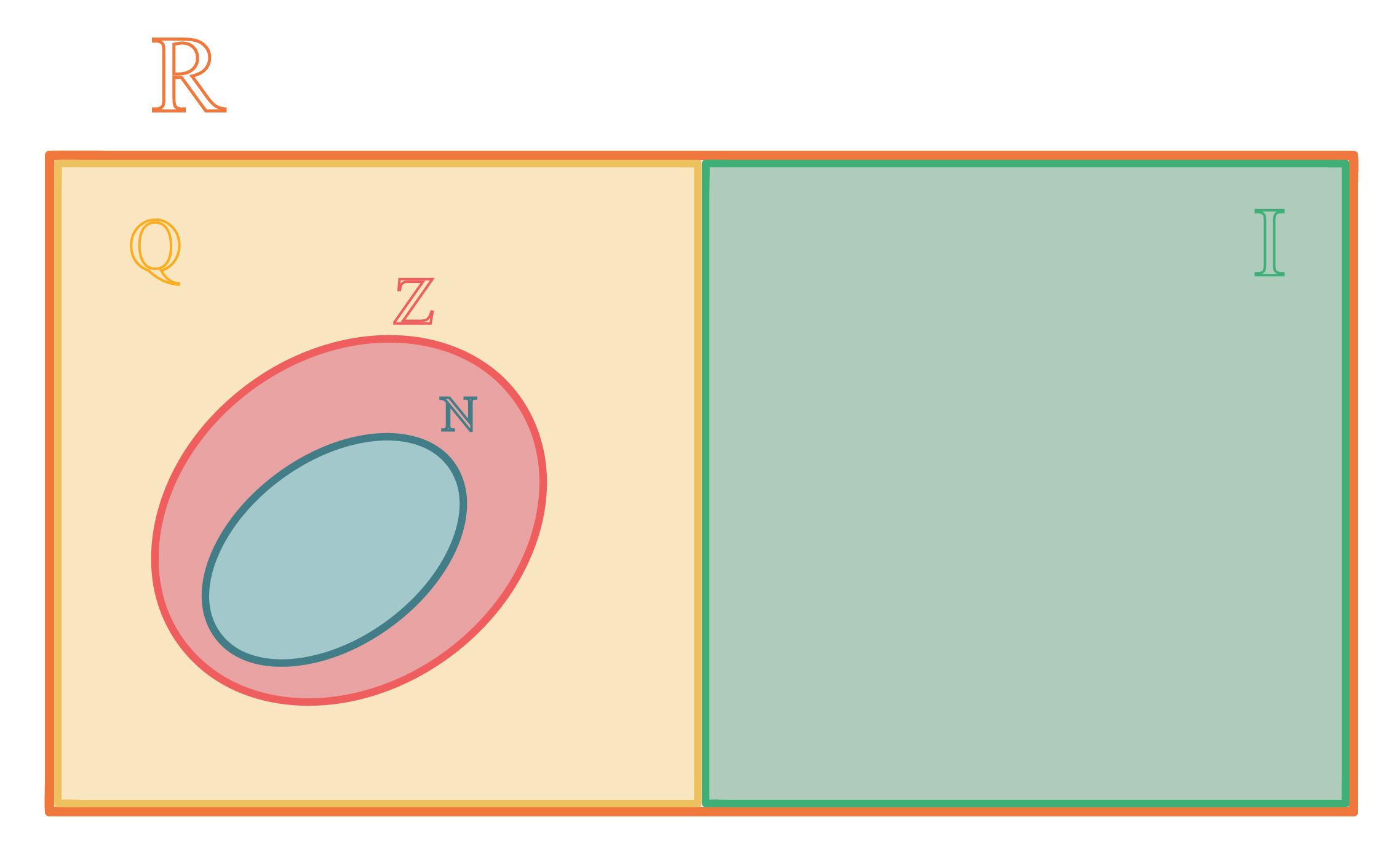
Além disso, com o advento dos números irracionais e reais, finalmente acabamos com as lacunas na reta real! Aliás, neste momento, o termo “reta real” ganha todo sentido. Se o conjunto dos números reais é formado por todos os números existentes, significa que podemos representar todo e qualquer número que desejarmos na reta. Com toda a certeza, esse número será racional ou irracional!

Atividades:
1. Marque a alternativa correta sobre o conjunto dos números irracionais.
A) O conjunto dos números irracionais é uma ampliação do conjunto dos números racionais, contendo os números racionais e também os números que não podem ser escritos como fração.
B) O conjunto dos números irracionais é formado por todos os números que não podem ser escritos na forma de fração. Assim, raízes não exatas e dízimas não periódicas fazem parte desse conjunto.
C) O conjunto dos números irracionais é formado por todos os números que podem ser representados na forma de fração, como os números decimais.
D) O conjunto dos números irracionais e o dos racionais são o mesmo conjunto.
2.Dos números irracionais a seguir, qual deles pertence ao intervalo 2 e 3?
A) Π
B) √2
C) √3
D) -3,123124458901...
E) √6
Classifique as afirmações a seguir como verdadeiras (V) ou falsas (F).
I – Um número inteiro pode ser um número irracional.
II – O conjunto dos números racionais tem intersecção vazia com o conjunto dos números irracionais.
III – O conjunto dos números irracionais está contido no conjunto dos números reais.
IV – O conjunto dos números reais está contido no conjunto dos números irracionais.
V – Qualquer raiz quadrada tem como resultado um número racional.
Marque a alternativa que contém a classificação correta das afirmativas respectivamente:
A) F, V, F, V, V
B) F, V, V, F , F
C) F, V, V, V ,F
D) F, F, F, F, V
E) V, F, F, V, V
Das alternativas abaixo, determine qual delas melhor se aproxima do valor do número irracional √8.
A) 2,830
B) 2,828
C) 2,826
D) 2,827
E) 2,831
Nenhum comentário:
Postar um comentário