NÚMEROS IRRACIONAIS
O conjunto dos números irracionais é formado pelos números que
não podem ser representados como frações. Em algumas situações,
o conjunto dos números racionais não era suficiente para a resolução de problemas,
foi quando se percebeu a existência dos números irracionais,
como as raízes não exatas, as dízimas não periódicas, o π, entre outros.
Conjunto dos números irracionais
No decorrer da história, na aplicação do teorema de Pitágoras em um triângulo
retângulo de lados medindo 1, percebeu-se que a resposta era igual à raiz do número 2.
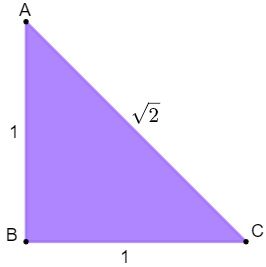
Acontece que essa resposta, aparentemente simples, tornou possível a descoberta
de um novo conjunto numérico.
Na tentativa de encontrar-se a resposta para essa raiz quadrada de 2,
encontrou-se um número decimal conhecido como dízima não periódica,
que é impossível de ser representada como uma fração.
Isso fez necessária a criação de um novo conjunto, os irracionais, já que,
até aquele momento, todos os números eram racionais (que podem escritos como fração).
O conjunto dos números irracionais é composto por todos os números que não podem ser escritos na forma de uma fração. |
Quais são os números irracionais?
Para que um número seja considerado irracional, ele precisa respeitar a definição,
ou seja, ele não pode ser representado como uma fração.
Esses números são as raízes não exatas,
as dízimas não periódicas e alguns casos especiais,
como a constante π (lê-se: pi) ou o número ɸ (lê-se: fi), entre outros.
Raízes não exatas
Quando o número não é um quadrado perfeito, é conhecido como raiz não exata.
Veja alguns exemplos:
![]()
Dízimas não periódicas
Ao resolver-se essas raízes, a resposta sempre vai ser uma aproximação,
o que chamamos de dízimas não periódicas.
![]()
Note que a parte decimal é infinita e que não existe um período, ou seja,
uma sequência que faça com que a gente consiga prever o
próximo número da parte decimal, e é por isso que chamamos esse número de dízima
não periódica. Não só as dízimas geradas por raízes não exatas, mas qualquer dízima
não periódica é um número irracional.
1. Associe os símbolos da coluna da esquerda com seu respectivo conjunto,
na coluna da direita:
a) números naturais ( ) Q
b) números racionais relativos ( ) Z
c) números inteiros relativos ( ) N
d) números reais ( ) R
2. Complete as lacunas escrevendo racionais ou irracionais.
a) Os números de representação decimal são:_________________
b) Os números de representação decimal infinita e periódica são:____________ .
c) Os números de representação decimal infinita e não periódica são: ________.
d) Os números naturais são: ________________.
e) Os números inteiros são:_____________.
f) As raízes não exatas são números: ______________.
g) As raízes exatas são números: ____________.
h) Os números ___________ podem ser escritos em forma de fração.
i) Os números ___________ não podem ser escritos em forma de fração.
3. Escreva Q para os racionais e I para os
irracionais:
a) 2,5
b) 0,666...
c) 3,2
d) 0,8
e) 2,236817...
f) 7
g) 1,732168...
h) 5,343434...

Nenhum comentário:
Postar um comentário